Depending on what mathematical requirements your application has, you may have to take special care to ensure that your operations return what you expect with respect to floating point (double) precision. For the JavaScript world at large, this isn't a new issue.
Find additional: JavaScript Articles
In fact, for the programming world at large, this isn't a new issue. JavaScript often gets bashed because “It can't perform math correctly.” If these same criteria were to be applied to C#, you'd reach the same conclusion. Later in this column, I'll illustrate how C# and JavaScript, as far as floating-point numbers are concerned, behave in the same way. In this edition's column, I take you through some of JavaScript's mathematical idiosyncrasies and how to work around them.
JavaScript's only native numeric type is the double-precision (floating point) 64-bit type.
Context and Core Concepts
If you're a developer in a place where JavaScript is not the primary language and you're tasked with something that requires JavaScript, whether on the client or server, you may have some already baked assumptions based on your primary experience with C, C#, VB, Ruby, Python, etc. Your first assumption is probably that JavaScript has an integer type. Your second assumption may be that JavaScript handles mathematical operations just like your primary language. Both assumptions are incorrect. The next question to address is WHY this is the case. To begin to answer that question, let's see JavaScript in action with a simple task, adding two values and testing for equality. Figure 1 shows a simple math problem.
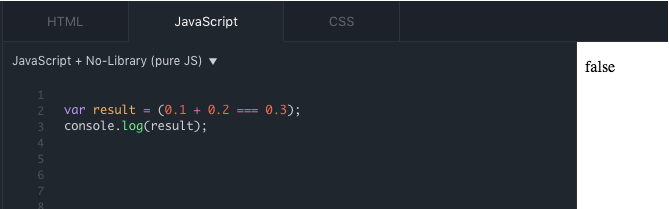
In C, C#, and other similarly situated languages, the result of 0.1 + 0 .2 == 0.3 is, of course, true. But that's not the case in JavaScript. Your next assumption may be that JavaScript can't do math. This would also be an incorrect assumption. Before you can understand how JavaScript behaves, you must first address what JavaScript is and more specifically what JavaScript is in the mathematical context and what numerical data types JavaScript directly supports.
The answer is just one. JavaScript supports one mathematical type, 64-bit floating point numbers. Because I'm talking about a 64-bit (binary) system, base 2 applies. The question to ask is “how are 64-bit floating point numbers stored?” The answer is that 64-bit floating point storage is divided into three parts, as shown in Figure 2.
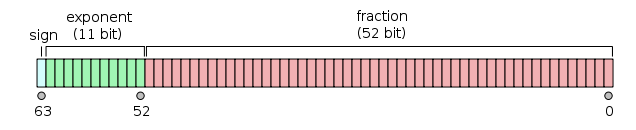
Reviewing the IEEE 754 standard, the largest integer that can safely be relied upon to be accurately stored is expressed as (253) – 1 or 9,007,199,254,740,991. Why do we need to subtract 1? The best way to explain that is to review the binary representation of 253 or 9,007,199,254,740,992, which looks like this:
0
00000000010
0000000000000000000000000000000000000000000000000000
Only the 10th bit is flipped. This 10th bit however, under the storage scheme illustrated in Figure 2 is in the bit range reserved for the exponent. Therefore, if you subtract 1 to get the largest safe integer value (9,007,199,254,740,991), the binary representation is as follows:
0
00000000001
1111111111111111111111111111111111111111111111111111
Bits 0 through 52 are flipped. Accordingly, this translates to the value 9,007,199,254,740,991. In JavaScript, there's a simple way to access this number and its negative counterpart with the MAX_SAFE_INTEGER and MIN_SAFE_INTEGER constants hosted in the Number Prototype, as shown in Figure 3.

To round out the illustration, the binary representation of the smallest safe integer value (-9,007,199,254,740,991) is represented as follows:
1
11111111110
0000000000000000000000000000000000000000000000
In this case, you simply reverse how the bits are flipped with respect to the largest safe integer value.
Now that you know how JavaScript supports the single numerical type and how its storage works from the smallest and largest integer perspective, turn your attention to the initial problem with decimals: 0.1 + 0.2 === .3 (the result being false). Perhaps you've heard the statement that floating point values cannot be guaranteed to be accurate. You certainly know this to be the case because the expression 0.1 + 0.2 === 0.3 is false in JavaScript. The question is: Why is it false?
You must first recognize that a computer can only natively store integers. That's the essence of the binary (base 2) nature of computing. For example, you have the following binary/decimal value pairs:
- 0 : 0
- 0 : 1
- 10 : 2
- 11: 3
- 100 : 4
- 101 : 5
- –
Outside of the computer, you routinely deal with numbers in base 10 system (every decimal point to the right is a reduction by a factor of 10). To get a non-repeating decimal result, your fraction must reduce to a denominator that is a prime factor of 10. The prime factors of 10 are 2 and 5. Using 1/2, 1/3, 1/4, and 1/5 as examples, when converting to decimal format, some are clean and terminating and some repeat. Accordingly, the preceding examples, converted to decimals, are as follows: .5, .33333333…., .25, and .2. In a base 10 system, as long as your divisor is evenly divisible by a prime factor of 10, you'll have a precise non-repeating result. Anything else repeats.
With a computer, there's the base 2 (binary) system of which there is only 1 factor, 2. This is the essence of a binary system; 0 or 1, on or off. There's no third option! This is why a computer can only natively store integers. Therefore, to get a finer level of precision via decimals, there must be a scheme within the operating bit range to represent such numbers. In the case with JavaScript, the scheme is 64 bit and Figure 2 illustrates how the scheme is divided between the left- and right-hand portions of the decimal point as well as the sign (positive or negative).
Why then does 0.1 + 0.2 != 0.3 in JavaScript? To begin to answer that question, let's see JavaScript in action in Figure 4.
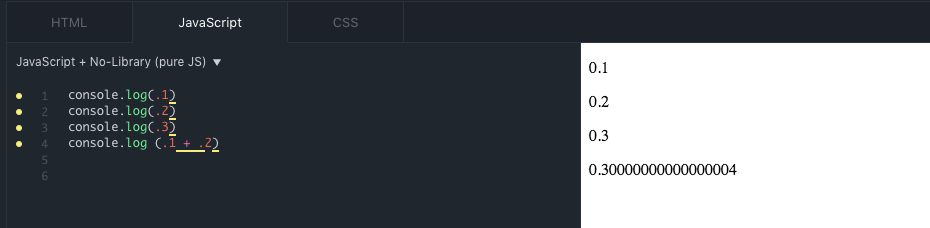
Figure 5 illustrates the same problem with C# .
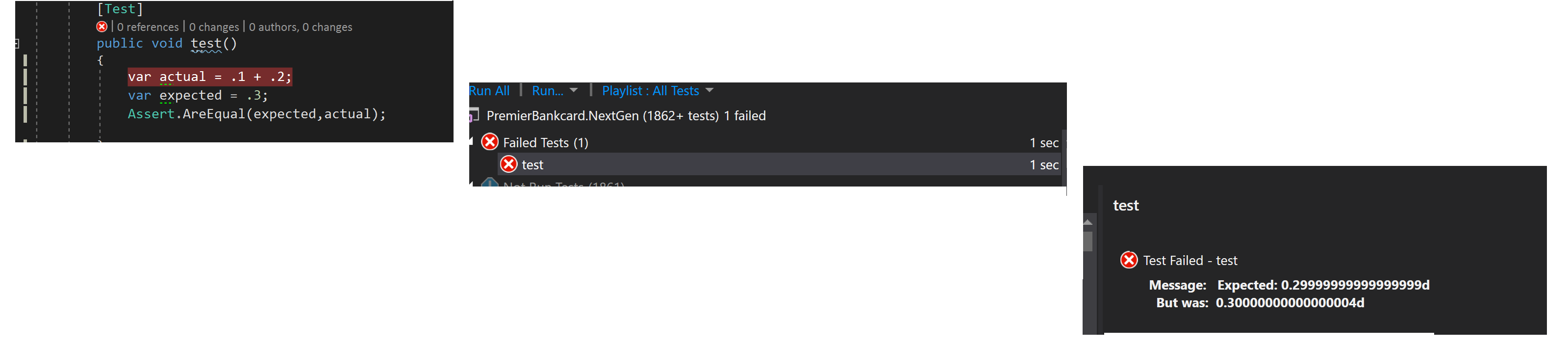
In reality, the values illustrated in Figure 5 are double precision types. If, in C#, you wish to treat the numbers as floats, you must use the “f” suffix, as in Figure 6.
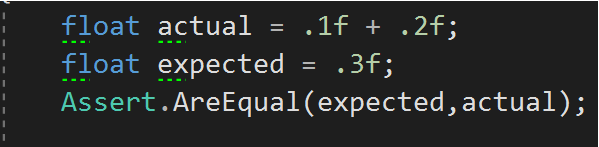
I'm referencing C# for two reasons. First, to illustrate when it's a like-for-like comparison with C#, the same problem can exist. Second, because languages like C# support multiple numeric types, there are ways in languages other than JavaScript to leverage other types to counteract the problem that may result from comparing floating types.
Returning to the core question in JavaScript, why does (.1 + .2) != .3? This gets to how decimals are stored as binary. Let's look at 0.1. As a fraction, .1 can be represented at 1/10. Everything a computer does must be broken down to binary. So then, what is .1 in binary? To answer that question, you have to take the fraction 1/10 and make it binary. The number 10 expressed as binary is 1010 (the 2nd and 4th bits—values 2 and 8—are flipped: 2 + 8 == 10). Therefore, the binary division is as follows: 1010/1. Have a look at Figure 7.

As you can see, 0011 infinitely repeats. Because there's only a finite space to store the infinitely repeating decimal, some accommodation has to be made. In order to fit within the bit constraint, 64 in this case, rounding must be applied. A useful site to bookmark can be found here: https://www.h-schmidt.net/FloatConverter/IEEE754.html. If you enter values for .1 and .2, you'll see the binary representation for those numbers and error values due to conversion. In this case, you see rounded error values of 1E-9 and 3E-9 for .1 and .2 respectively. Accordingly, when you see the result of .1 + .2, it shouldn't be surprising to see the rounding error being carried forward; in this case for .1 + .2, you see a difference in the final result illustrated in Figure 4.
JavaScript performs arithmetic calculations with floating point numbers in a manner consistent with other programming languages.
Application
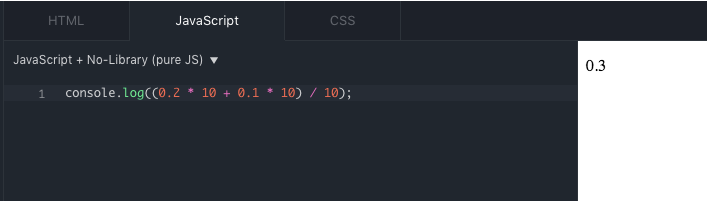
What's a developer to do? Does this mean if you have mathematical operations to perform, JavaScript is useless? Of course not. The real issue is floating point/double precision numbers themselves and how errors can creep in when converted to and from binary format. One way to address the problem is to first take the floating-point aspect of things away and instead, work with derived integers and then dividing the result. Figure 8 illustrates a way to resolve the problem.
If you really wish to geek-out on floating points, consider reviewing this article by David Goldberg entitled “What Every Computer Scientist Should Know About Floating Point Arithmetic” (https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html).
Another approach you may wish to consider is a service endpoint that's backed up by a language such as C, C#, VB, Ruby, Python, etc. Regardless of which approach you take, it's important to recognize, as early as possible, your application's potential sensitivity to precision problems with floating point numbers. In all cases, and especially this case, testing is your friend!
Key Takeaways
What's a developer to do? Does this mean if you have mathematical operations to perform, JavaScript is useless? Of course not. The real issue is the floating point/double precision numbers themselves and how errors can creep in when converted to and from binary. Regardless of the language environment, caution must be exercised when dealing with floating point numbers because not all real numbers can be exactly represented as floating point numbers. One solution is to simply not use floating point numbers. For JavaScript, that's difficult because the only number JavaScript has is the floating point. In cases where monetary operations are necessary, your best approach may very well be to let a back-end service handle your calculations and then pass data back to JavaScript as a string for display purposes. It all depends on what your specific application requires. If all you deal with are whole numbers that exist between the min and max safe integers in Figure 3, you shouldn't run into the issues described in this article.
If that's not the case and instead you deal with decimals, consider using a library like decimal.js: https://github.com/MikeMcl/decimal.js/. It's important to understand and recognize that issues with floats exist. And if you think it isn't a matter of life or death, then consider what happened on February 25, 1991. On that day, there was a Patriot Missile failure. The Patriot Missile launch failed to intercept a Scud Missile, which lead to the death of 28 U.S. Army personnel. The cause? Lack of precision in floating point numbers stored in a 24-bit register: http://www-users.math.umn.edu/~arnold/disasters/patriot.html.



