AccelerateTM for Microsoft 365 is a new, commercially available Microsoft Office add-in that deeply integrates the Visual Scheme for ApplicationsTM (VSATM) programming language into the popular back-office automation suite, for versions 2016 and later. VSA intends to serve as the “third musketeer,” alongside Visual Basic for Applications (VBA) and the popular formula expression language of Excel, but with a twist: Under the hood of this uniquely powerful language is the full reach and power of the .NET Framework.
VSA is implemented on top of .NET and woven directly into the fabric of the storied Office suite via the Accelerate for Microsoft 365 add-in. Initial focus is on Excel, but eventually all the applications that are part of the suite will benefit from its core value proposition. The add-in supports in-application scripting in VSA via a proper REPL (see Figure 1), available from within the host Office application (and accessible at the command line as well for external processing).
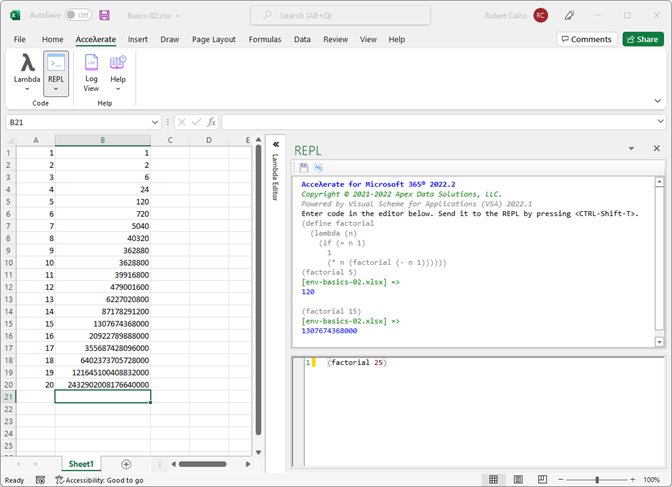
In the case of Excel, an additional pretty-printing, syntax-highlighting Lambda Editor (see Figure 2) makes writing user-defined functions (UDFs) in Scheme both easy and convenient.
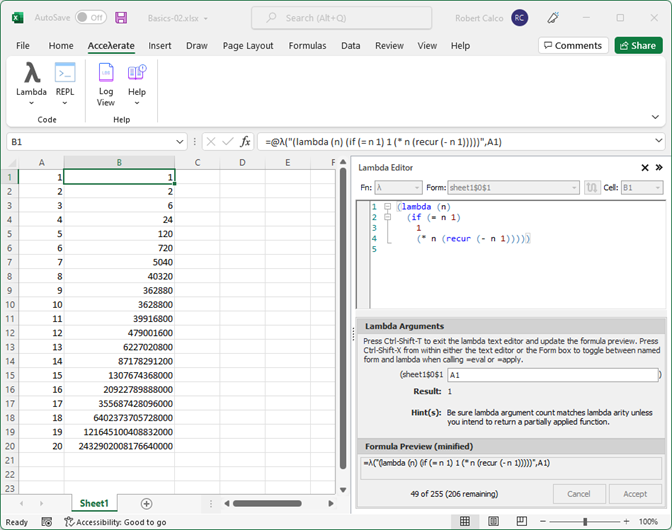
In this latter capacity within Excel, Visual Scheme for Applications compliments Microsoft's recent addition of the LET() and LAMBDA() functions to their formula expression language by providing a flavor of the same functional programming approach to creating UDFs, but with an external enterprise integration focus. Unlike the formula expression language in which LET() and LAMBDA() are available, VSA code can interact with the outside world from both directions: the inside out and the outside in. A standalone scripting engine at the command line for general-purpose programming accompanies the add-in and comes with a plethora of useful Scheme and .NET wrapper libraries for this very purpose.
In this article, I'll walk you through the rationale for making Scheme on .NET a first-class extension/automation language of the Office suite by way of a hands-on primer. First, I'll cover some basic facts about Scheme as I ease into reviewing VSA as a first-class language for user-defined function (UDF) development in Excel. Then, I'll explore some of the more powerful techniques around wrapping .NET libraries for use in VSA-powered Office solutions. Finally, I'll take a step back and cover syntax extensions, perhaps the most mystifying feature of the language, and how to interact with them in the built-in and command-line REPL.
Why Scheme?
At first glance, Scheme might seem an odd choice of a language to tag team with VBA and Excel's formula expression language. On closer inspection, and especially considering Microsoft's new, explicitly “functional programming” direction with Excel's formula expression language, Scheme seems the inevitable choice.
Scheme is a seasoned dialect in the venerable Lisp family of computer programming languages. Quoting Guy Steele, one of Scheme's inventors, “If you give someone FORTRAN, he has FORTRAN. If you give someone Lisp, he has any language he pleases” (Friedman, D. The Reasoned Schemer, Second Edition, MIT Press, 1998). The choice of providing a Lisp language is a conscious decision to put the programmer in control of the language's features and functions for a given domain. The bottom-up style of programming it encourages results in every Lisp application becoming a domain-specific language (DSL). This is because of a feature that all Lisps have, called macros (although Scheme's flavor of this feature is unique to it, and referred to as “syntax extension” instead). I'll show an example of this below.
The choice of providing a Lisp language is a conscious decision to put the programmer in control of the language's features
andfunctions for a given domain.
Many top-flight universities teach Scheme to first-year computer science majors with no previous background in programming, because anyone can grasp its basic syntax in just a few hours. It's very easy to learn (and to teach), with an approachable and consistent core syntax based on Lisp S-expressions that's both very succinct and surprisingly malleable. Mastering Scheme is a bit like mastering chess, with the exception that even a complete beginner can do amazing things in Scheme right away.
The Scheme that Accelerate for Microsoft 365 integrates into Office goes by the name “Visual Scheme for Applications,” or VSA, making its mission clear: to be the perfect companion to VBA, by adding metaprogramming power and .NET reach to the Office/VBA solution developer's arsenal of tools.
It's worth noting briefly that Scheme is used elsewhere in the real world. For example, the Scheme programming language is the GNU project's official application extension language, where it goes by the name of Guile (see: https://gnu.org/software/guile). Another implementation of Scheme, called MIT Scheme, is the programming language of choice for teaching, using several advanced textbooks on diverse engineering topics, including classical mechanics (Structure and Interpretation of Classical Mechanics, by G.J. Sussman and J. Wisdom), differential geometry (Functional Differential Geometry, by G.J. Sussman and J. Wisdom), and software engineering (Software Design for Flexibility - How to Avoid Programming Yourself into a Corner, by C. Hanson, and G.J. Sussman). In other words, Scheme is more at home in application extensions, math-intensive, and data-intensive problem domains than you may realize. Sounds perfect for Office - especially Excel!
Yet another popular embodiment of Scheme goes by the name of Racket (see https://www.racket-lang.org). Racket aspires to be an industrial-strength Scheme whose main mission is “language-oriented programming,” proving that Scheme is indeed a uniquely powerful language for creating DSLs.
All of these facts make Scheme, at the very least, an intriguing choice for Office solutions developers looking for ways to modernize their clients' back-office systems in an interconnected, multi-cloud world.
So, let's see it in action, shall we?
Mary Had a Little (lambda () ...)
One thing that surprises developers who haven't yet had a chance to explore a proper Lisp is how similar the new LET/LAMBDA functions in Excel look, or at least feel, like Lisp/Scheme. Here is an example of an Excel LAMBDA/LET function:
=LAMBDA(X,Y,LET(XS,X*X,YS,Y*Y,SQRT(XS+YS)))
Now here's the same thing in Scheme:
(lambda (x y)
(let ((xs (* x x))
(ys (* y y)))
(sqrt (+ xs ys))))
To make it a little bit clearer how a Schemer would almost automatically see the original LAMBDA/LET function by formatting it a more semantically revealing way, consider:
=LAMBDA(X, Y, LET(XS, X*X, YS, Y*Y, SQRT(XS+YS)))
That looks a lot like Scheme to me! The only real difference is the infix notation and the semantics of the LET expression, which one simply must know to understand what's going on. The evaluation order is not particularly self-evident unless, of course, you happen to know how the let binding form in every Lisp works.
The beauty of the Scheme code is that syntactically there's a lot less going on, and no foreknowledge is required to understand it. The Scheme prefix notation makes commas unnecessary and there's zero ambiguity about what each set of parentheses do in context. The values are evaluated according to the natural structure of the nested S-expressions. A Schemer understands that the parentheses, far from being an annoyance, serve this disambiguation function and make so much syntax seem superfluous when it's related to order precedence and other grammar rules that most languages need to define and enforce somehow.
One thing that surprises developers who haven't yet had a chance to explore a proper Lisp is how similar the new LET/LAMBDA functions in Excel look, or at least feel, like Lisp/Scheme.
In the LAMBDA function, by contrast, it's necessary to simply know that the LET function MUST have an odd number of parameters, the last of which must evaluate to a value and the arguments you provide must alternate between a name and a value binding.
Now let's take a quick look at some of the more meat-and-potatoes uses of lambda expressions in Accelerate for Microsoft 365.
Figure 3 is a screenshot of an example spreadsheet provided in the download zip file (available in the download for this article) that captures several important idioms of programming in Scheme as well as a simple example of .NET interoperability. The challenge is to compose sentences from words listed in 2D regions. In the first region, the words are ordered by row, which is Excel's default evaluation order when feeding a region to a user-defined function. The second region orders the words by column.
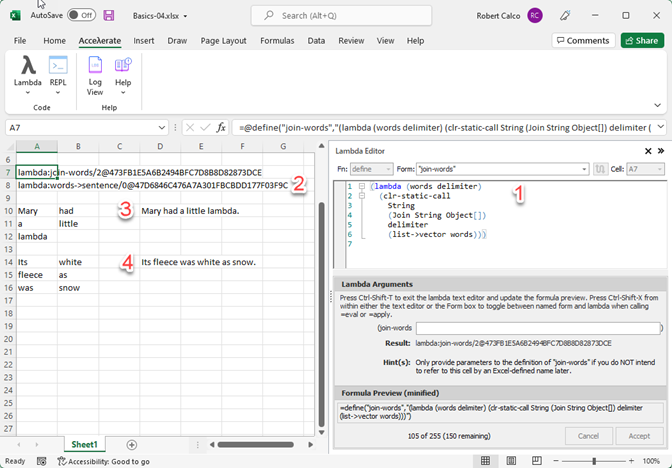
There are four listings where lambda expressions are added to the sheet, corresponding to the numbers in Figure 3.
Listing 1 is the “join-words” lambda expression. In the sheet, this is created using the =define function provided by the add-in. It allows you to give a Scheme name to a lambda expression. The resulting expression in A7 tells you that the Scheme name and the arity (or number of arguments) it takes. The hash is computed every time the code is altered to trigger Excel's calculation engine (depending on what options for auto-calculation you have set up) and can be ignored.
Listing 1: the “join-words” lambda expression
(lambda (words delimiter)
(clr-static-call String (Join String Object[]) delimiter (list->vector words)))
Note the clr-static-call form. This is one of several .NET interop forms that are built in, making it easy for you to call into the .NET runtime directly. In this case, you're calling the static Join method of the String class in the System namespace.
The tricky bit here is that, as you can see by the signature, Join expects an array, not a list. So, you call the built-in list->vector Scheme function on “words,” which does just what it says: It converts a list to a vector. Vectors in Scheme are the same as arrays in .NET.
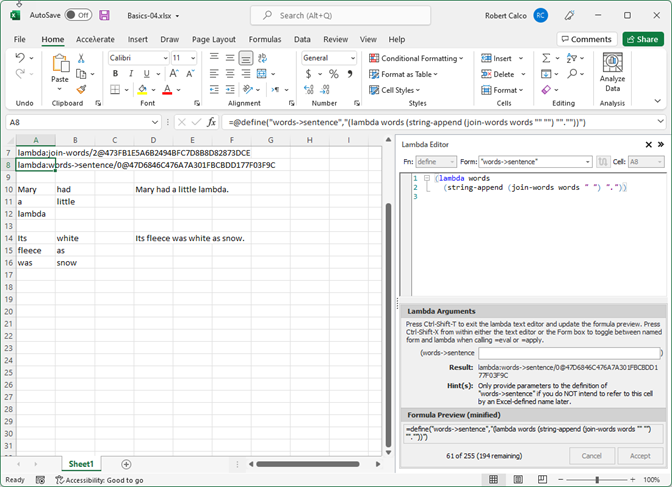
Listing 2 (shown in the Lambda Editor in Figure 4) is the words->sentence lambda expression, which uses join-words to produce all but the final period on the sentence. String-append is used to add that. This expression is variadic, which you can tell by the fact that the sole argument is the word words with no parentheses around it. This means that it can take zero or more arguments, and wraps whatever is (or isn't) sent up into a nice list that =apply can use.
Listing 2: the “words->sentence” lambda expression
(lambda words (string-append (join-words words " ") "."))
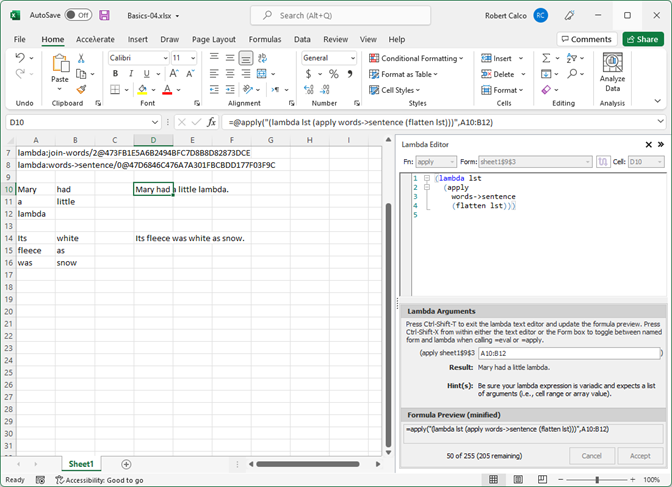
Listing 3 (shown in the Lambda Editor in Figure 5) uses the =eval function provided by the add-in with a lambda expression that, in turn, calls the built-in =apply form. The issue here is that =apply can only accept a single list, of whatever type is required by the function to which it is applying the list. Excel is sending a 2D array or region, and so it's necessary to flatten the input to pass a list as expected by =apply.
Listing 3: using (flatten lol) in an inline “apply” lambda
(lambda lst (apply words->sentence (flatten lst)))
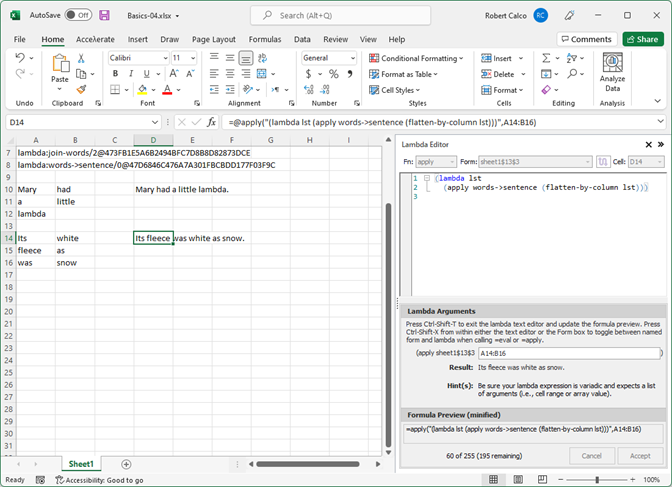
Listing 4 (shown in the Lambda Editor in Figure 6) is nearly identical, except that flatten-by-column is used instead to obtain the correct word order in the sentence it creates.
Listing 4: using (flatten-by-column lol) in an inline “apply” lambda
(lambda lst (apply words->sentence(flatten-by-column lst)))
Although somewhat contrived, this example shows some important idioms and how they map to conventional Excel behavior that's important to understand.
Never Block the Chain
The add-in comes with a tutorial walking you through creating a blockchain-like feature in Excel. Figure 7 is a screenshot of the first part of that tutorial.
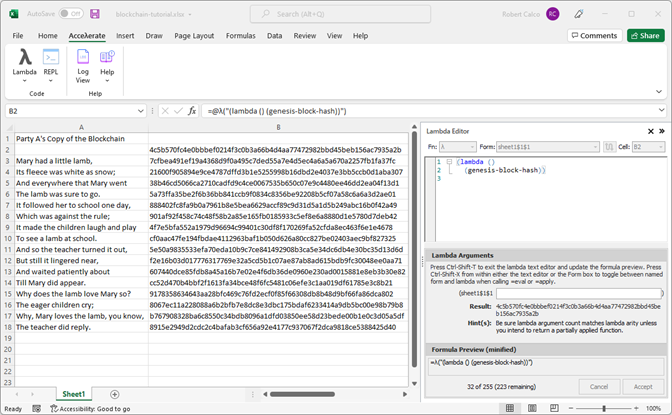
Rather than duplicate the steps here, instead I'll briefly cover the salient aspects of the code that's produced by the end of the tutorial (see Listing 5). The two things that should be paid most attention are:
- The direct interop with .NET via
clr-*functions - How .NET abstractions are wrapped in idiomatic Scheme code in a library, conformant with the R6RS Scheme specification
Listing 5: blockchain.sls
(library (blockchain)
(export string->sha256
data-mine
genesis-block
genesis-block-hash)
(import (ironscheme)
(ironscheme clr))
(clr-using System.Text)
(clr-using System.Security.Cryptography)
(define genesis-block (make-parameter "This is my genesis block."))
(define genesis-block-hash (lambda () (string->sha256 (genesis-block))))
(define string->sha256 (lambda (str)
(let* ((utf8 (clr-static-prop-get Encoding UTF8))
(bytes (clr-call UTF8Encoding (GetBytes String) utf8 str))
(hash-fn (clr-new SHA256Managed))
(raw-result (clr-call SHA256Managed
(ComputeHash System.Byte[]) hash-fn bytes))
(bits-str (clr-static-call BitConverter ToString raw-result))
(clean-bits (clr-call String Replace bits-str "-" ""))
(lower-bits (clr-call String ToLower clean-bits)))
lower-bits)))
(define data-mine (lambda (current-block-data previous-block-hash)
(let* ((combined-data (string-append current-block-data "+"
previous-block-hash))
(result (string->sha256 combined-data)))
result)))
)
All of the code to make this example work is stored in the blockchain.sls library file (the full contents of which are provided in Listing 5). The only code that you'll find in the sample spreadsheet that's included in the download is a lambda expression to grab the genesis block hash in B2.
(lambda ()
(genesis-block-hash))
The rest of the calls use the =eval function provided by the add-in calling the "data-mine" function that's defined in Listing 5 with the appropriate arguments. These are the data of the current block and the hash of the previous block, respectively.
=eval("data-mine",A3,B2)
The tutorial does a good job of developing the code, so I'll just comment on the important highlights of Listing 5.
First, blockchain.sls is a canonical library definition per the R6RS specification, with which VSA and the underlying IronScheme implementation is 99% compliant. There are some niche aspects of continuations - a powerful Scheme feature that allows the language to be used to program constructs of other languages - that simply can't be implemented on the CLR because of low-level restrictions.
It exports and imports several symbols from the (ironscheme clr) namespace. The various clr-* forms encountered in Listing 5 are part of a very straightforward CLR interoperability API that you, as a VSA coder, will get to know quickly, because the code here exercises most of it and is relatively easy to understand.
The (clr-using ...) form works just like the C# using or VB.NET imports statements. It allows the library to reference symbols in the respective namespaces.
The genesis-block symbol is a Scheme parameter. This is similar to a dynamic variable in Lisp or a global variable in JavaScript, intended to allow a default value that is mutable, but the normal use of parameters is to give them locally scoped values that don't affect the global default value once the local value is out of scope.
Parameter values in Scheme are obtained by calling them like a function with no arguments. Setting them to new values is done by passing in a single argument, the new value. At creation time, Scheme parameters can have “guards” that will test any new value and disallow anything that should not be permitted as a new value.
By far the most interesting symbol in Listing 5 is the string->sha256 symbol.
(define string->sha256
(lambda (str)
(let* ((utf8 (clr-static-prop-get Encoding UTF8))
(bytes (clr-call UTF8Encoding (GetBytes String) utf8 str))
(hash-fn (clr-new SHA256Managed))
(raw-result (clr-call SHA256Managed (ComputeHash System.Byte[])
hash-fn bytes))
(bits-str (clr-static-call BitConverter ToString raw-result))
(clean-bits (clr-call String Replace bits-str "-" ""))
(lower-bits (clr-call String ToLower clean-bits)))
lower-bits)))
This function takes a string, and calls into the .NET System.Security.Cryptography and System.Text namespaces to produce a SHA256 hash of the string, and is massaged to appear in the required format. It's worth taking time to work through this tutorial, because it's representative of what developers will do to surface .NET in a concise, easy-to-use way in the context of Excel formula expressions.
Anything You Can Do, I Can Do Meta
Finally, let's take a look at a Scheme syntax extension.
While the team was wrapping .NET APIs, it became desirable to iterate over collections implementing the IEnumerable interface in a cleaner syntax. Listing 6 provides the full code. What follows will be only a high-level description, as an entire series of articles could be written to properly explain how you might write code like this. It cannot be stressed enough just how powerful syntax extensions are in Scheme.
Listing 6: The built-in (define-enumerable ...) syntax extension
(define-syntax define-enumerable (lambda (x)
(syntax-case x (as)
((_ enum-name enum-fn)
#'(define-enumerable enum-name enum-fn as IEnumerable))
((_ enum-name enum-fn as enum-type)
#'(define enum-name
(case-lambda [() (let ((iter (enum-fn)))
(make-iterator (lambda () (unless iter
(set! iter
(clr-call enum-type
GetEnumerator
(enum-fn))))
(clr-call IEnumerator MoveNext iter))
(lambda ()
(clr-prop-get IEnumerator Current iter))
(lambda ()
(set! iter (clr-call enum-type GetEnumerator
(enum-fn))))))]
[(obj) (let ((iter (enum-fn obj)))
(make-iterator
(lambda ()
(unless iter
(set! iter (clr-call enum-type
GetEnumerator
(enum-fn obj))))
(clr-call IEnumerator MoveNext iter))
(lambda ()
(clr-prop-get IEnumerator Current iter))
(lambda ()
(set! iter (clr-call enum-type
GetEnumerator
(enum-fn obj))))))]))))))
Most .NET developers will recall the sense of wonder and awe the first time the C# compiler team released LINQ, or “Language Integrated Query.” Most will also remember the gradual evolution of LINQ into the powerful, general-purpose DSL that it is today. What I am about to say is not meant to diminish that sense of awe, but rather to rekindle it.
In Scheme, a mostly complete version of LINQ can be implemented in a weekend in about 900 lines of pure Scheme code.
You heard that right. This may sound blasphemous to a .NET developer. However, any veteran Lisper or Schemer will know that this is a fair observation. We are used to such power at our fingertips - it's the whole point of the language.
We know this because that's the true story of the (ironscheme linq) library that's included as part of VSA. This is NOT a wrapper of .NET's LINQ features, which are specific to compilers that implement them, but rather a pure Scheme implementation of generic iterators against pure Scheme collections with most of the familiar syntax sugar .NET developers will recognize instantly.
Unfortunately, because it wasn't a wrapper of .NET, it left the team in a bind. There was no way to use IEnumerable collections with this pure Scheme iterator implementation. This isn't really a bind for a language like Scheme. Listing 6 allowed you to bridge the gap and use .NET collections with the pure-Scheme LINQ by defining pure Scheme iterators wrapping the IEnumerable interface, which, on the surface, looks completely compatible.
In Scheme, a mostly complete version of LINQ can be implemented in a weekend in about 900 lines of pure Scheme code.
To be fair, Listing 6 is considerably more complicated than we thought it would be. It turns out, IEnumerable is not implemented in a uniform way for what appear to be mainly historical reasons, as the interface was treated - even by Microsoft - as more of a suggestion than a contract. In particular, the Reset() method often produces surprising behavior depending on how the implementor of a collection that supports IEnumerable decided to handle this. In order to deal with this, we had to make the syntax extension, named (define-enumerable ...), able to take different input based on the caller's understanding of the object they're dealing with. Some classes that implement IEnumerable do what you need them to do, but sadly this isn't something you can take for granted. The VSA team found it necessary to provide default functionality obtaining a fresh IEnumerable instance from the parent object in which it was defined. It's not pretty, but it works, and you have the option to provide a specific type to cast it to when you know it does the right thing.
Example usages below come from the (visualscheme data rdf core) library.
The first example is the wrapper of the AllNodes property of a Graph class as defined in dotNetRDF. (RDF plays an important role in the Professional edition but is also available in the Standard edition.) Basically, what the (define-enumerable...) syntax needs is a function to obtain the fresh collection either from the (current-graph) by default, or a specific graph instance passed in via the one-argument version of the method.
(define-enumerable graph/all-nodes
(case-lambda
[() (clr-prop-get Graph AllNodes (current-graph))]
[(graph) (begin
(if (or (null? graph) (not (graph? graph)))
(error "graph must be a non-null Graph.")
(if (not (eq? graph (current-graph))) (current-graph graph)))
(clr-prop-get Graph AllNodes graph))]))
The following snippet is similar, except to get it to work for triples of a Graph, you have to provide an explicit type to which it needs to be cast so that the appropriate Reset() behavior is obtained - in this case, TreeIndexedTripleCollection.
(define-enumerable graph/triples (case-lambda
[() (clr-prop-get Graph Triples (current-graph))]
[(graph)
(begin
(if (or (null? graph) (not (graph? graph)))
(error "graph must be a non-null Graph.")
(if (not (eq? graph (current-graph))) (current-graph graph)))
(clr-prop-get Graph Triples graph))]) as TreeIndexedTripleCollection)
These allow the user of the wrapper code to write the following:
(foreach t in (graph/triples)
(display t)
(newline))
Listing 7 provides a fuller flavor of LINQ in VSA, all of which will now also work with .NET types that implement IEnumerable if you use define-enumerable, as you did above, to expose them to IronScheme's iterator framework. These are borrowed from the documentation in (ironscheme linq) written by Llewelyn Pritchard, the main developer of IronScheme on which VSA is based.
Listing 7: Some LINQ examples in Scheme
;; conformance to C# tests
;; simply permutations of the grammar and matched to the output
;; of C#
(define (print-list lst)
(foreach x in lst (printf "~a, " x))
(printf "\n"))
(define selectdata '(1 5 3 4 2))
(define groupdata '(2 5 2 4 2))
(define nestdata '((2 5)(2 4)(3 5)(3 1)(1 1)))
(define a (from x in selectdata select x))
(print-list a)
(define a2 (from x in (from y in selectdata select (+ y 1))
select (- x 1)))
(print-list a2)
(define b (from x in selectdata
where (even? x)
select x))
(print-list b)
(define c (from x in selectdata
orderby x
select x))
(print-list c)
(define d (from x in selectdata
orderby x descending
select x))
(print-list d)
(define e (from x in selectdata
where (odd? x)
orderby x
select x))
(print-list e)
(define f ( from x in selectdata
let y = (* x x)
select y))
(print-list f)
(define f2 (from x in selectdata
let y = (* x x)
where (odd? y)
orderby y descending
select y))
(print-list f2)
(define g (from x in selectdata
select x into z
select z))
(print-list g)
(define h (from x in nestdata
from y in x
select y))
(print-list h)
(define i (from x in nestdata
where (= (car x) 2)
from y in x
select y))
(print-list i)
(define j (from x in nestdata
orderby (car x)
from y in x
select y))
(print-list j)
(define k (from x in nestdata
from y in x
orderby y
select y))
(print-list k)
(define l (from x in nestdata
select x into y
from z in y
select z))
(print-list l)
(define m (from x in nestdata
group (car x) by (cadr x)))
(print-list m)
(define n (from x in nestdata
group (cadr x) by (car x)))
(print-list n)
(define o (from x in nestdata
group (cadr x) by (car x) into z
select z))
(print-list o)
(define p (from x in nestdata
group (cadr x) by (car x) into z
orderby (key z) descending
select z))
(print-list p)
(define q (from x in selectdata
join y in groupdata on x equals y into z
from w in z
select w))
(print-list q)
(define r (from x in selectdata
join y in groupdata on x equals y
select (cons x y)))
(print-list r)
(define s (from x in selectdata
from y in groupdata
where (and (= x 4) (= y 2))
select (cons x y)))
(print-list s)
(define t (from x in selectdata
join y in groupdata on x equals y into z
orderby x
select z))
(print-list t)
(define u (from x in selectdata
join y in groupdata on x equals y into z
orderby x
select (cons x z)))
(print-list u)
(define v (from x in selectdata
from y in groupdata
select y into z
where (even? z)
select z))
(print-list v)
I Said All That So I Can Say This…
This novel combination of a proven functional programming language designed from the ground-up for metaprogramming with the vast ecosystem of the .NET Runtime in all its incarnations means that Office solution developers suddenly have access to two broad and deep solution spaces that previously were unavailable.
The sturdy yet shape-shifting Scheme language offers a way to harness and control the raw power of the Common Language Runtime. It will be exciting to see how industrious Office power users, VBA coders, Schemers, and .NET developers work together to leverage it and achieve greater returns for themselves and their clients.




